class: center, middle, inverse, title-slide # Linear model with single predictor<br> 🍡 ### Dr. Çetinkaya-Rundel --- layout: true <div class="my-footer"> <span> Dr. Mine Çetinkaya-Rundel - <a href="https://introds.org" target="_blank">introds.org </a> </span> </div> --- class: center, middle # Interpreting models --- ## Height & width .small[ ```r m_ht_wt <- lm(Height_in ~ Width_in, data = pp) tidy(m_ht_wt) ``` ``` ## # A tibble: 2 x 5 ## term estimate std.error statistic p.value ## <chr> <dbl> <dbl> <dbl> <dbl> ## 1 (Intercept) 3.62 0.254 14.3 8.82e-45 ## 2 Width_in 0.781 0.00950 82.1 0. ``` ] -- `$$\widehat{Height_{in}} = 3.62 + 0.78~Width_{in}$$` -- - **Slope:** For each additional inch the painting is wider, the height is expected to be higher, on average, by 0.78 inches. -- - **Intercept:** Paintings that are 0 inches wide are expected to be 3.62 inches high, on average. The intercept is meaningless in the context of these data, it only serves to adjust the height of the line. --- ## Linear model with a single predictor - We're interested in `\(\beta_0\)` (population parameter for the intercept) and `\(\beta_1\)` (population parameter for the slope) in the following model: $$ \hat{y} = \beta_0 + \beta_1~x $$ -- - But we don't have access to the population, so we use sample statistics to estimate them: $$ \hat{y} = b_0 + b_1~x $$ -- - Another way of describing this model is $$y = b_0 + b_1~x + e $$ --- ## Least squares regression - The regression line minimizes the sum of squared residuals. -- - If `\(e_i = y - \hat{y}\)`, then, the regression line minimizes `\(\sum_{i = 1}^n e_i^2\)`. --- ## Properties of the least squares regression line - The regression line goes through the center of mass point, the coordinates corresponding to average `\(x\)` and average `\(y\)`: `\((\bar{x}, \bar{y})\)`: `$$\hat{y} = b_0 + b_1 x ~ \rightarrow ~ b_0 = \hat{y} - b_1 x$$` -- - The slope has the same sign as the correlation coefficient: `\(b_1 = r \frac{s_y}{s_x}\)` -- - The sum of the residuals is zero: `\(\sum_{i = 1}^n e_i = 0\)` -- - The residuals and `\(x\)` values are uncorrelated. --- ## Height & landscape features ```r m_ht_lands <- lm(Height_in ~ factor(landsALL), data = pp) tidy(m_ht_lands) ``` ``` ## # A tibble: 2 x 5 ## term estimate std.error statistic p.value ## <chr> <dbl> <dbl> <dbl> <dbl> ## 1 (Intercept) 22.7 0.328 69.1 0. ## 2 factor(landsALL)1 -5.65 0.532 -10.6 7.97e-26 ``` -- `$$\widehat{Height_{in}} = 22.68 - 5.65~landsALL$$` --- ## Height & landscape features (cont.) - **Slope:** Paintings with landscape features are expected, on average, to be 5.65 inches shorter than paintings that without landscape features. - Compares baseline level (`landsALL = 0`) to other level (`landsALL = 1`). - **Intercept:** Paintings that don't have landscape features are expected, on average, to be 22.68 inches tall. --- ## Categorical predictor with 2 levels ``` ## # A tibble: 8 x 3 ## name price landsALL ## <chr> <dbl> <dbl> ## 1 L1764-2 360 0 ## 2 L1764-3 6 0 ## 3 L1764-4 12 1 ## 4 L1764-5a 6 1 ## 5 L1764-5b 6 1 ## 6 L1764-6 9 0 ## 7 L1764-7a 12 0 ## 8 L1764-7b 12 0 ``` --- ## Relationship between height and school ```r m_ht_sch <- lm(Height_in ~ school_pntg, data = pp) tidy(m_ht_sch) ``` ``` ## # A tibble: 7 x 5 ## term estimate std.error statistic p.value ## <chr> <dbl> <dbl> <dbl> <dbl> ## 1 (Intercept) 14. 10.0 1.40 0.162 ## 2 school_pntgD/FL 2.33 10.0 0.232 0.816 ## 3 school_pntgF 10.2 10.0 1.02 0.309 ## 4 school_pntgG 1.65 11.9 0.139 0.889 ## 5 school_pntgI 10.3 10.0 1.02 0.306 ## 6 school_pntgS 30.4 11.4 2.68 0.00744 ## 7 school_pntgX 2.87 10.3 0.279 0.780 ``` -- .question[ Where did all these new predictors come from? ] --- ## Categorical explanatory variables with 3+ levels - When the categorical explanatory variable has many levels, they're encoded to **dummy variables**. - Each coefficient describes the expected difference between heights in that particular school compared to the baseline level. .midi[ ``` ## # A tibble: 7 x 5 ## term estimate std.error statistic p.value ## <chr> <dbl> <dbl> <dbl> <dbl> ## 1 (Intercept) 14. 10.0 1.40 0.162 ## 2 school_pntgD/FL 2.33 10.0 0.232 0.816 ## 3 school_pntgF 10.2 10.0 1.02 0.309 ## 4 school_pntgG 1.65 11.9 0.139 0.889 ## 5 school_pntgI 10.3 10.0 1.02 0.306 ## 6 school_pntgS 30.4 11.4 2.68 0.00744 ## 7 school_pntgX 2.87 10.3 0.279 0.780 ``` ] -- .question[ What is the baseline level? ] --- .question[ `landsALL` had two levels: 0 and 1. What was the baseline level for the model with `landsALL` as predictor? ] ``` ## # A tibble: 2 x 5 ## term estimate std.error statistic p.value ## <chr> <dbl> <dbl> <dbl> <dbl> ## 1 (Intercept) 22.7 0.328 69.1 0. ## 2 factor(landsALL)1 -5.65 0.532 -10.6 7.97e-26 ``` --- .question[ `school` has 7 levels: A = Austrian, D/FL = Dutch/Flemish, F = French, G = German, I = Italian, S = Spanish, X = Unknown. What us the baseline level for the model with `school` as predictor? ] ``` ## # A tibble: 7 x 5 ## term estimate std.error statistic p.value ## <chr> <dbl> <dbl> <dbl> <dbl> ## 1 (Intercept) 14. 10.0 1.40 0.162 ## 2 school_pntgD/FL 2.33 10.0 0.232 0.816 ## 3 school_pntgF 10.2 10.0 1.02 0.309 ## 4 school_pntgG 1.65 11.9 0.139 0.889 ## 5 school_pntgI 10.3 10.0 1.02 0.306 ## 6 school_pntgS 30.4 11.4 2.68 0.00744 ## 7 school_pntgX 2.87 10.3 0.279 0.780 ``` --- ## Dummy coding ``` ## # A tibble: 7 x 7 ## # Groups: school_pntg [7] ## school_pntg D_FL F G I S X ## <chr> <int> <int> <int> <int> <int> <int> ## 1 A 0 0 0 0 0 0 ## 2 D/FL 1 0 0 0 0 0 ## 3 F 0 1 0 0 0 0 ## 4 G 0 0 1 0 0 0 ## 5 I 0 0 0 1 0 0 ## 6 S 0 0 0 0 1 0 ## 7 X 0 0 0 0 0 1 ``` --- ## Interpretation of coefficients .question[ Interpret the intercept, slope for Dutch/Flemish, slope for Spanish paintings. ] ``` ## # A tibble: 7 x 5 ## term estimate std.error statistic p.value ## <chr> <dbl> <dbl> <dbl> <dbl> ## 1 (Intercept) 14. 10.0 1.40 0.162 ## 2 school_pntgD/FL 2.33 10.0 0.232 0.816 ## 3 school_pntgF 10.2 10.0 1.02 0.309 ## 4 school_pntgG 1.65 11.9 0.139 0.889 ## 5 school_pntgI 10.3 10.0 1.02 0.306 ## 6 school_pntgS 30.4 11.4 2.68 0.00744 ## 7 school_pntgX 2.87 10.3 0.279 0.780 ``` --- ## The linear model with multiple predictors - Population model: $$ \hat{y} = \beta_0 + \beta_1~x_1 + \beta_2~x_2 + \cdots + \beta_k~x_k $$ -- - Sample model that we use to estimate the population model: $$ \hat{y} = b_0 + b_1~x_1 + b_2~x_2 + \cdots + b_k~x_k $$ --- ## Correlation does not imply causation! 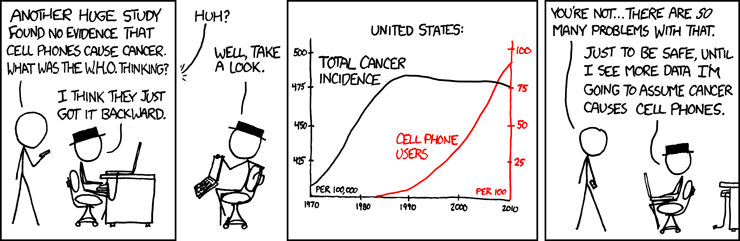Remember this when interpreting model coefficients <br> <img src="img/cell_phones.png" width="100%" /> .footnote[ Source: XKCD, [Cell phones](https://xkcd.com/925/) ] --- class: center, middle # Prediction with models --- ## Predict height from width .question[ On average, how tall are paintings that are 60 inches wide? `\(\widehat{Height_{in}} = 3.62 + 0.78~Width_{in}\)` ] -- ```r 3.62 + 0.78 * 60 ``` ``` ## [1] 50.42 ``` -- "On average, we expect paintings that are 60 inches wide to be 50.42 inches high." -- **Warning:** We "expect" this to happen, but there will be some variability. (We'll learn about measuring the variability around the prediction later.) --- ## Prediction in R Use the `predict()` function to make a prediction: - First argument: model - Second argument: data frame representing the new observation(s) for which you want to make a prediction, with variables with the same names as those to build the model, except for the response variables --- ## Prediction in R (cont.) - Making a prediction for a single new observation: ```r newpainting <- tibble(Width_in = 60) predict(m_ht_wt, newdata = newpainting) ``` ``` ## 1 ## 50.46919 ``` - Making a prediction for multiple new observations: ```r newpaintings <- tibble(Width_in = c(50, 60, 70)) predict(m_ht_wt, newdata = newpaintings) ``` ``` ## 1 2 3 ## 42.66123 50.46919 58.27715 ``` --- ## Prediction vs. extrapolation .question[ On average, how tall are paintings that are 400 inches wide? 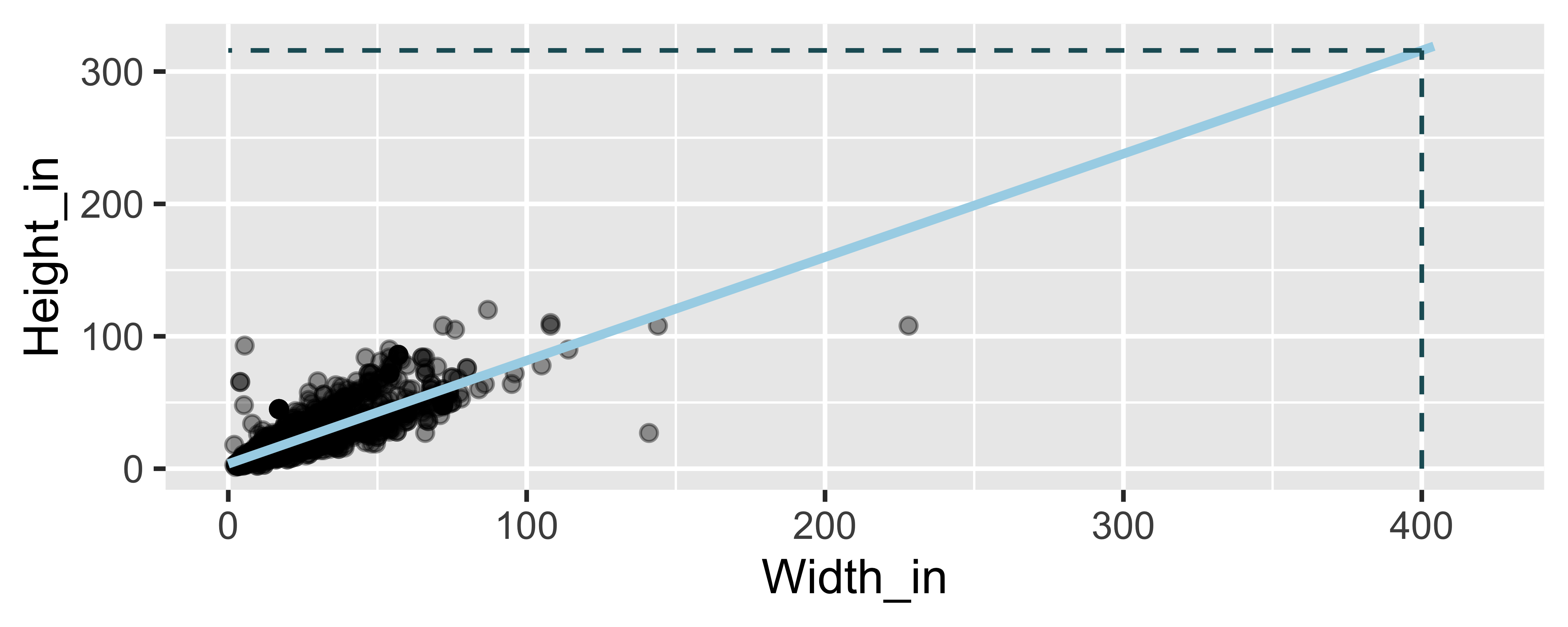`$$\widehat{Height_{in}} = 3.62 + 0.78~Width_{in}$$` ] <img src="w7_d2-linear-model-single-predictor_files/figure-html/extrapolate-1.png" width="1500" /> --- ## Watch out for extrapolation! > "When those blizzards hit the East Coast this winter, it proved to my satisfaction that global warming was a fraud. That snow was freezing cold. But in an alarming trend, temperatures this spring have risen. Consider this: On February 6th it was 10 degrees. Today it hit almost 80. At this rate, by August it will be 220 degrees. So clearly folks the climate debate rages on."¹ <br> Stephen Colbert, April 6th, 2010 .footnote[ [1] OpenIntro Statistics. "Extrapolation is treacherous." OpenIntro Statistics. ] --- class: center, middle # Measuring model fit --- ## Measuring the strength of the fit - The strength of the fit of a linear model is most commonly evaluated using `\(R^2\)`. - It tells us what percent of variability in the response variable is explained by the model. - The remainder of the variability is explained by variables not included in the model. --- ## Height vs. lanscape features .question[ Which of the following is the correct interpretation of `\(R^2\)` of the model below. ] .small[ ```r m_ht_lands <- lm(Height_in ~ factor(landsALL), data = pp) glance(m_ht_lands)$r.squared ``` ``` ## [1] 0.03456724 ``` ] **(a)** 3.5% of the variability in heights of painting can be explained by whether or not the painting has landscape features. **(b)** 3.5% of the variability in whether a painting has landscape features can be explained by heights of paintings. **(c)** This model predicts 3.5% of heights of paintings accurately. **(d)** This model predicts 3.5% of whether a painting has landscape features accurately. **(e)** 3.5% of the time there is an association between whether a painting has landscape features and its height. --- ## Height vs. width .small[ ```r glance(m_ht_wt) ``` ``` ## # A tibble: 1 x 11 ## r.squared adj.r.squared sigma statistic p.value df logLik AIC ## <dbl> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl> ## 1 0.683 0.683 8.30 6749. 0 2 -11083. 22173. ## # … with 3 more variables: BIC <dbl>, deviance <dbl>, df.residual <int> ``` ```r glance(m_ht_wt)$r.squared # extract R-squared ``` ``` ## [1] 0.6829468 ``` ] Roughly 68% of the variability in heights of paintings can be explained by their widths. --- class: center, middle # Tidy regression output --- ## Not-so-tidy regression output - You might come accross these in your googling adventures, but we'll try to stay away from them - Not because they are wrong, but because they don't result in tidy data frames as results. --- ## Not-so-tidy regression output (1) #### Option 1: ```r m_ht_wt ``` ``` ## ## Call: ## lm(formula = Height_in ~ Width_in, data = pp) ## ## Coefficients: ## (Intercept) Width_in ## 3.6214 0.7808 ``` --- ## Not-so-tidy regression output (2) #### Option 2: ```r summary(m_ht_wt) ``` ``` ## ## Call: ## lm(formula = Height_in ~ Width_in, data = pp) ## ## Residuals: ## Min 1Q Median 3Q Max ## -86.714 -4.384 -2.422 3.169 85.084 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 3.621406 0.253860 14.27 <2e-16 ## Width_in 0.780796 0.009505 82.15 <2e-16 ## ## Residual standard error: 8.304 on 3133 degrees of freedom ## (258 observations deleted due to missingness) ## Multiple R-squared: 0.6829, Adjusted R-squared: 0.6828 ## F-statistic: 6749 on 1 and 3133 DF, p-value: < 2.2e-16 ``` --- ## Review .question[ What makes a data frame tidy? ] -- - Each variable forms a column. - Each observation forms a row. - Each type of observational unit forms a table. --- ## Tidy regression output Achieved with functions from the broom package: - `tidy`: Constructs a data frame that summarizes the model's statistical findings: coefficient estimates, *standard errors, test statistics, p-values*. - `glance`: Constructs a concise one-row summary of the model. This typically contains values such as `\(R^2\)`, adjusted `\(R^2\)`, *and residual standard error that are computed once for the entire model*. - `augment`: Adds columns to the original data that was modeled. This includes predictions and residuals. --- ## We've already seen... - Tidy your model's statistical findings .small[ ```r tidy(m_ht_wt) ``` ``` ## # A tibble: 2 x 5 ## term estimate std.error statistic p.value ## <chr> <dbl> <dbl> <dbl> <dbl> ## 1 (Intercept) 3.62 0.254 14.3 8.82e-45 ## 2 Width_in 0.781 0.00950 82.1 0. ``` ] - Glance to assess model fit .small[ ```r glance(m_ht_wt) ``` ``` ## # A tibble: 1 x 11 ## r.squared adj.r.squared sigma statistic p.value df logLik AIC ## <dbl> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl> ## 1 0.683 0.683 8.30 6749. 0 2 -11083. 22173. ## # … with 3 more variables: BIC <dbl>, deviance <dbl>, df.residual <int> ``` ] --- ## Augment data with model results New variables of note (for now): - `.fitted`: Predicted value of the response variable - `.resid`: Residuals .small[ ```r augment(m_ht_wt) %>% slice(1:5) ``` ``` ## # A tibble: 5 x 10 ## .rownames Height_in Width_in .fitted .se.fit .resid .hat .sigma ## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> ## 1 1 37 29.5 26.7 0.166 10.3 3.99e-4 8.30 ## 2 2 18 14 14.6 0.165 3.45 3.96e-4 8.31 ## 3 3 13 16 16.1 0.158 -3.11 3.61e-4 8.31 ## 4 4 14 18 17.7 0.152 -3.68 3.37e-4 8.31 ## 5 5 14 18 17.7 0.152 -3.68 3.37e-4 8.31 ## # … with 2 more variables: .cooksd <dbl>, .std.resid <dbl> ``` ] -- .question[ Why might we be interested in these new variables? 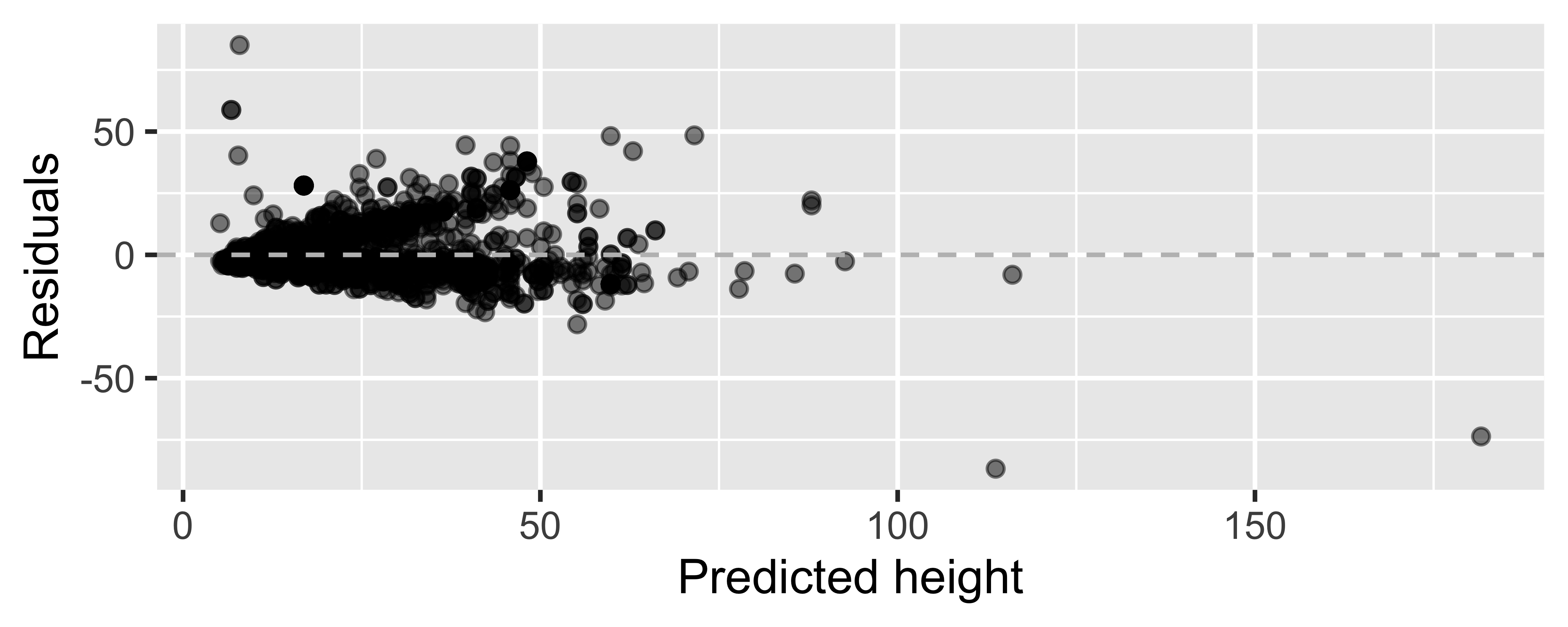] --- ## Residuals plot .small[ ```r m_ht_wt_aug <- augment(m_ht_wt) ggplot(m_ht_wt_aug, mapping = aes(x = .fitted, y = .resid)) + geom_point(alpha = 0.5) + geom_hline(yintercept = 0, color = "gray", lty = 2) + labs(x = "Predicted height", y = "Residuals")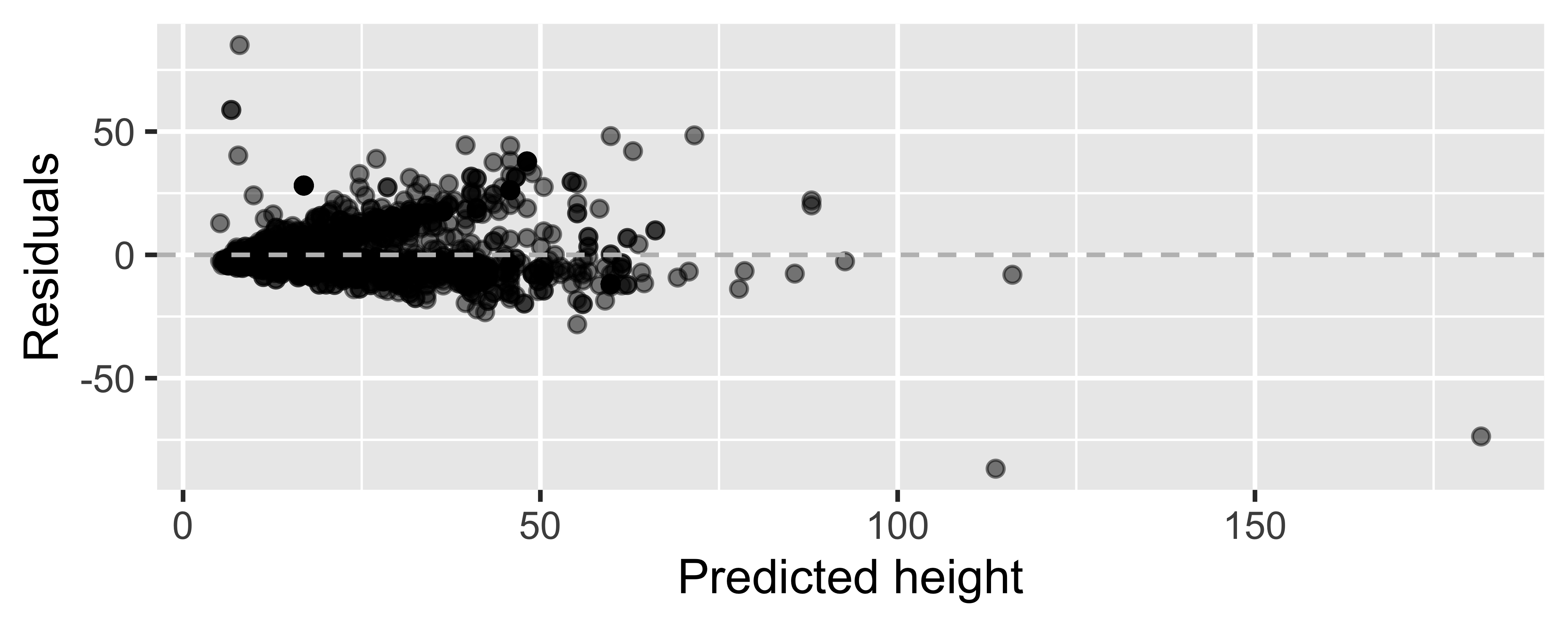 ``` <img src="w7_d2-linear-model-single-predictor_files/figure-html/unnamed-chunk-20-1.png" width="1500" /> ] --- class: center, middle # Model checking --- ## "Linear" models - We're fitting a "linear" model, which assumes a linear relationship between our explanatory and response variables. - But how do we assess this? 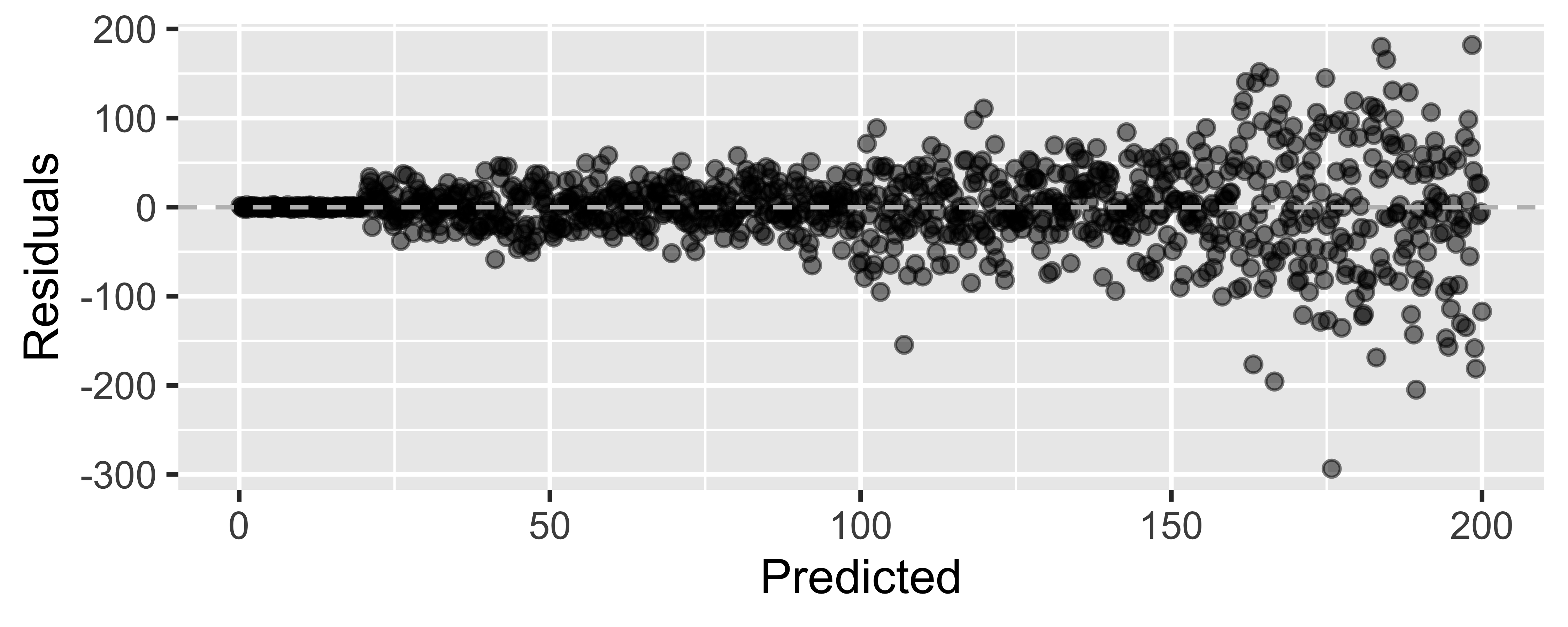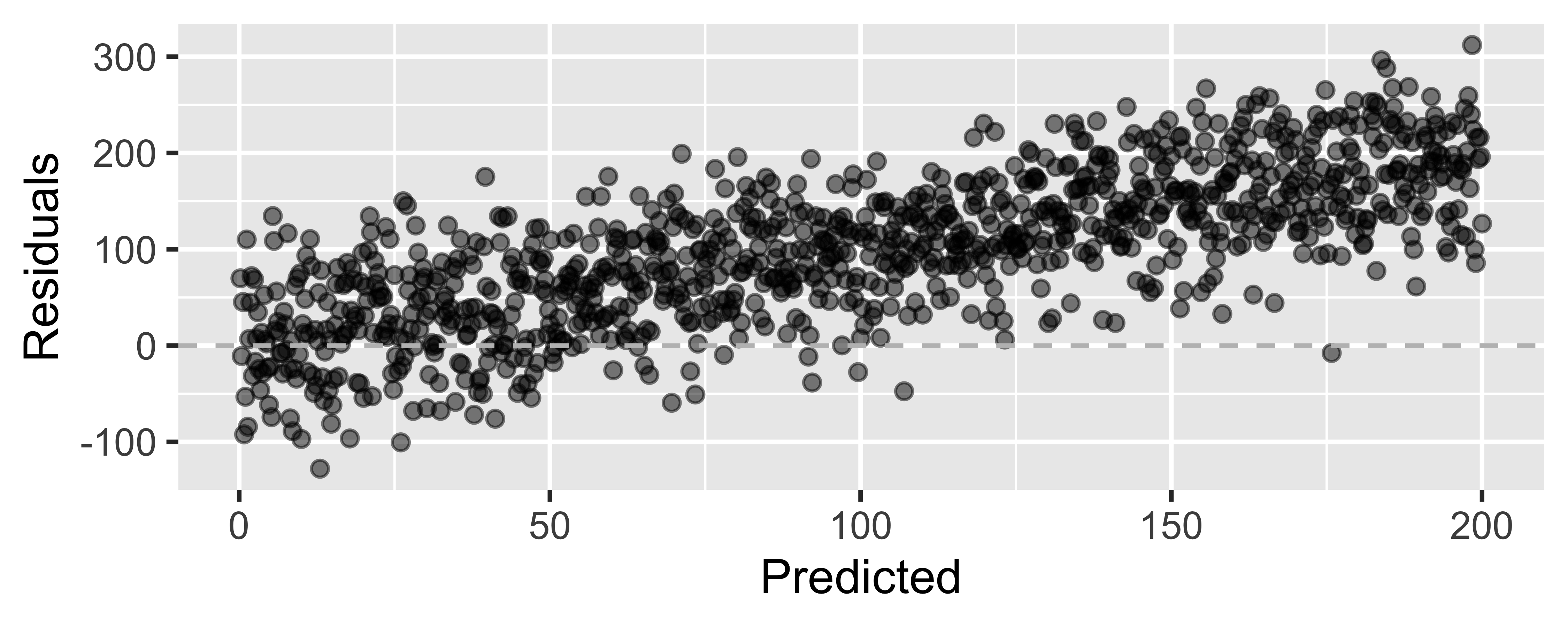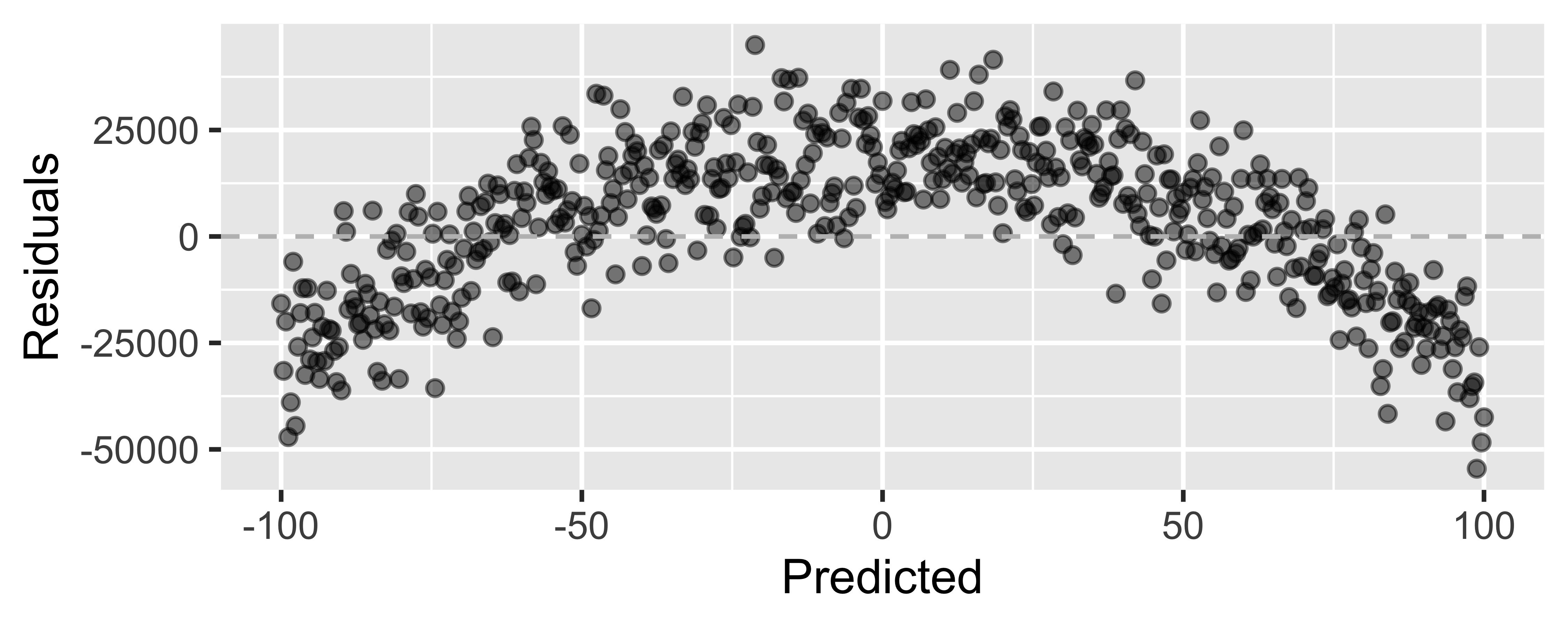--- ## Looking for... - Residuals distributed randomly around 0 - With no visible pattern along the x or y axes <img src="w7_d2-linear-model-single-predictor_files/figure-html/unnamed-chunk-21-1.png" width="1500" /> --- ## Not looking for... 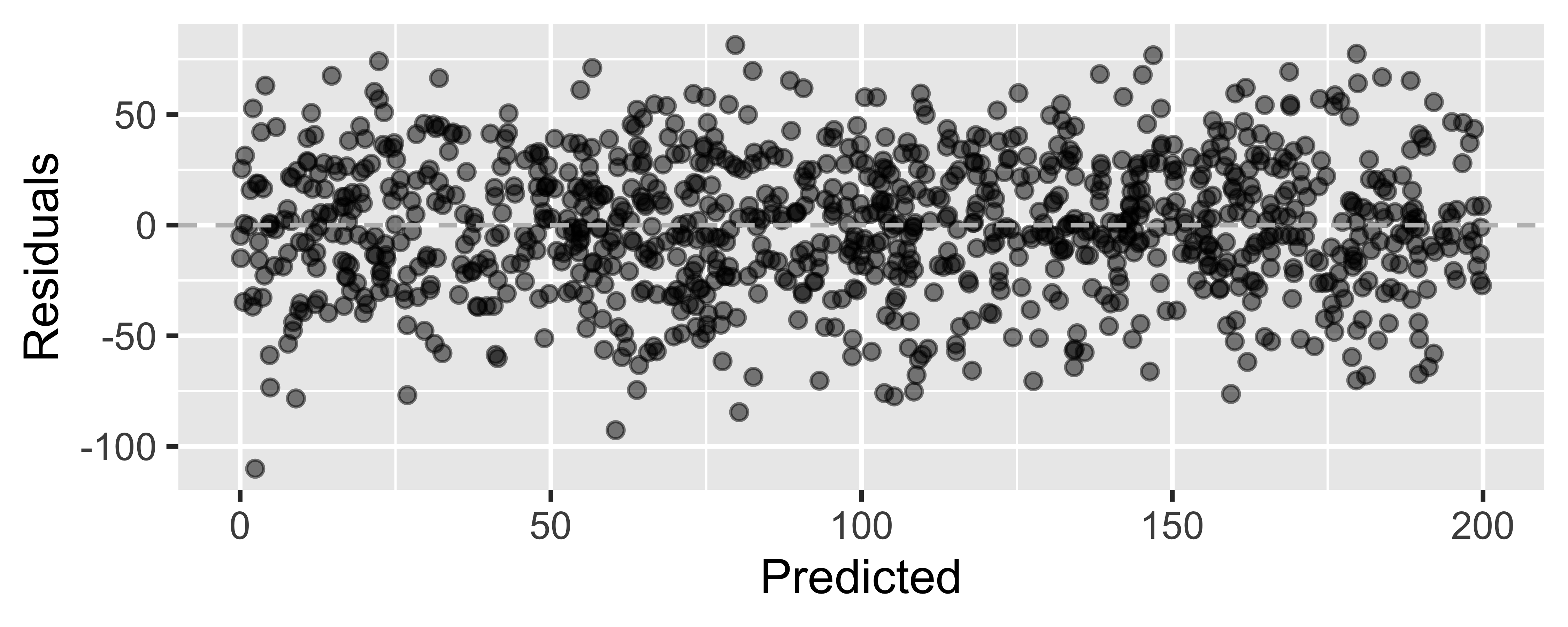### Fan shapes <img src="w7_d2-linear-model-single-predictor_files/figure-html/unnamed-chunk-22-1.png" width="1500" /> --- ## Not looking for... ### Residuals correlated with predicted values <img src="w7_d2-linear-model-single-predictor_files/figure-html/unnamed-chunk-23-1.png" width="1500" /> --- ## Not looking for... ### Groups of patterns <img src="w7_d2-linear-model-single-predictor_files/figure-html/unnamed-chunk-24-1.png" width="1500" /> --- ## Not looking for... ### Any patterns! 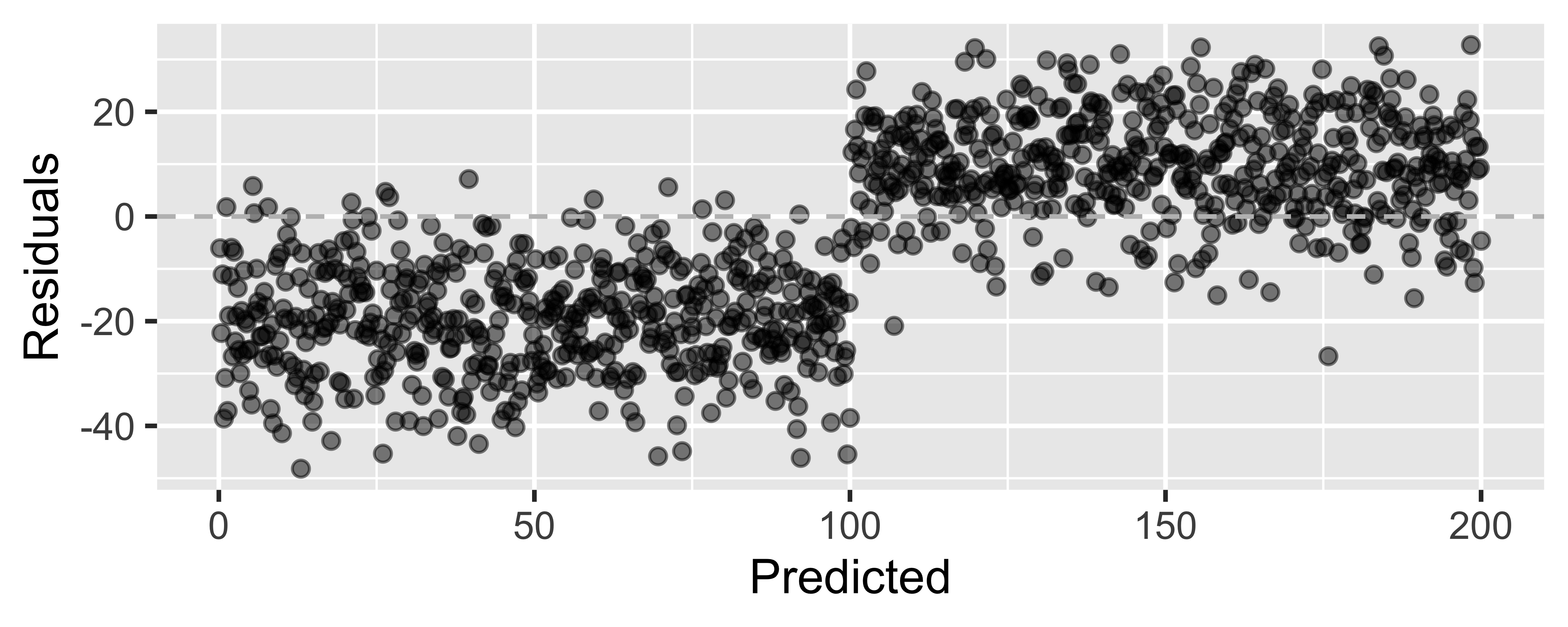<img src="w7_d2-linear-model-single-predictor_files/figure-html/unnamed-chunk-25-1.png" width="1500" /> --- .question[ What patterns does the residuals plot reveal that should make us question whether a linear model is a good fit for modeling the relationship between height and width of paintings? ] <img src="w7_d2-linear-model-single-predictor_files/figure-html/unnamed-chunk-26-1.png" width="1500" />