Model selection
⛏
Dr. Çetinkaya-Rundel
Announcements
- Student hours:
- Tuesdays - 14:30 - 15:30 at JCMB 2257
- Wednesdays - 14:30 - 15:30 online at bit.ly/ids-zoom
- Until 26 Nov 2019
- Peer evaluations: round 2 due Tue 12 Nov at 17:00 (tomorrow)
- Project proposal revisions (optional): due today Mon 11 Nov at 17:00 (tomorrow)
From last time
- Model selection follows Occam's Razor: among competing hypotheses that predict equally well, the one with the fewest assumptions should be selected.
- We use adjusted R-squared to compare the strength of fit of models (as opposed to R-squared) since adjusted R-squared applies a penalty for additional variables included in the model, and only goes up if the predictive contribition of an additional explanatory variable is higher than the penalty it brings along.
Backwards elimination
- Start with full model (including all candidate explanatory variables and all candidate interactions)
- Remove one variable at a time, record the adjusted R-squared for each of the resulting models, and selected the model with the highest adjusted R-squared
- Continue until adjusted R-squared does not increase
Forward selection
- Start with empty model
- Add one variable (or interaction effect) at a time, record the adjusted R-squared for each of the resulting models, and select the model with the highest adjusted R-squared
- Continue until adjusted R-squared does not increase
Data load & prep
evals <- read_csv("data/evals-mod.csv")evals <- evals %>% mutate(bty_avg = rowMeans(select(., bty_f1lower:bty_m2upper)))Starting small: score ~ cls_did_eval + cls_students + cls_perc_eval
What percent of the variability in evaluation scores is explained by the model?
full_model <- lm(score ~ cls_did_eval + cls_students + cls_perc_eval, data = evals)glance(full_model)$r.squared## [1] 0.04463827glance(full_model)$adj.r.squared## [1] 0.03839408library(GGally)evals %>% select(score, cls_did_eval, cls_students, cls_perc_eval) %>% ggpairs()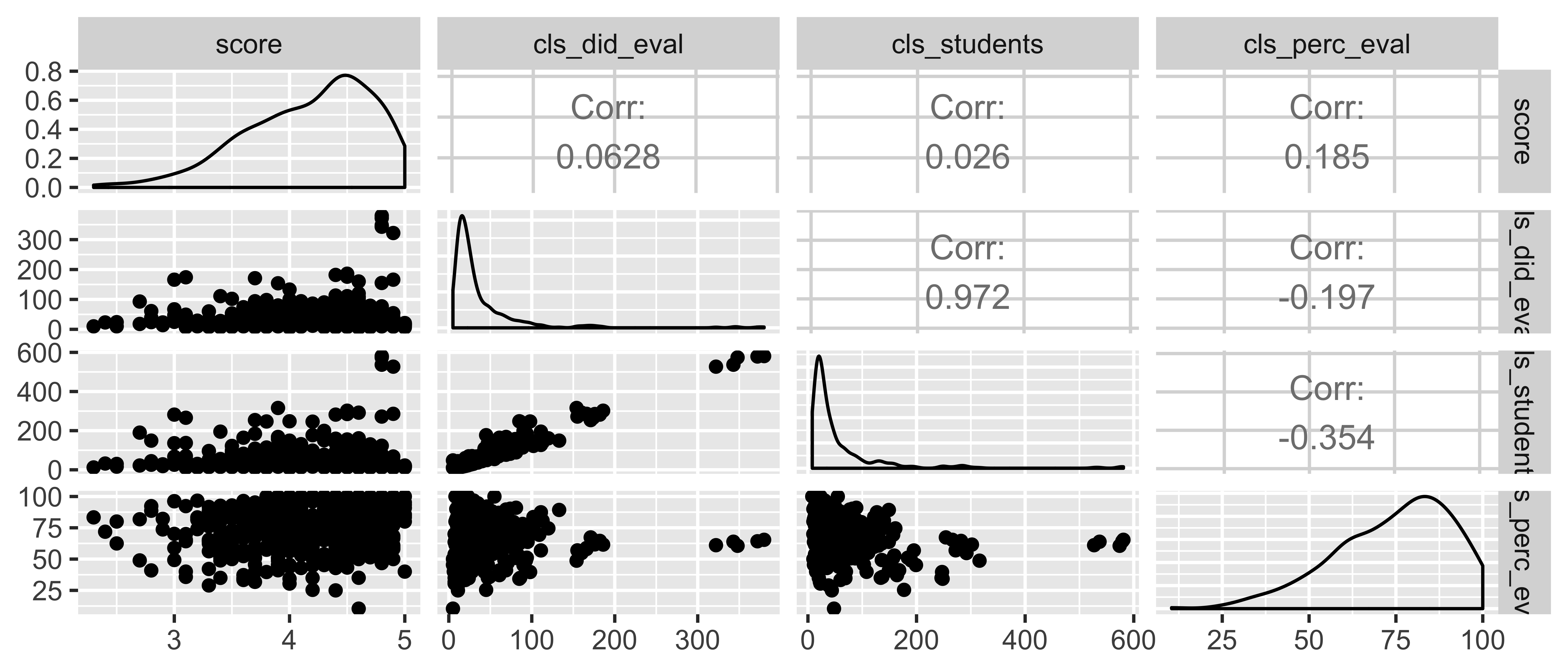
Suppose we definitely want to keep cls_did_eval in the model. Which of the
other two variables (cls_students or cls_perc_eval) is least likely to
be effective in increasing the model's predictive power?
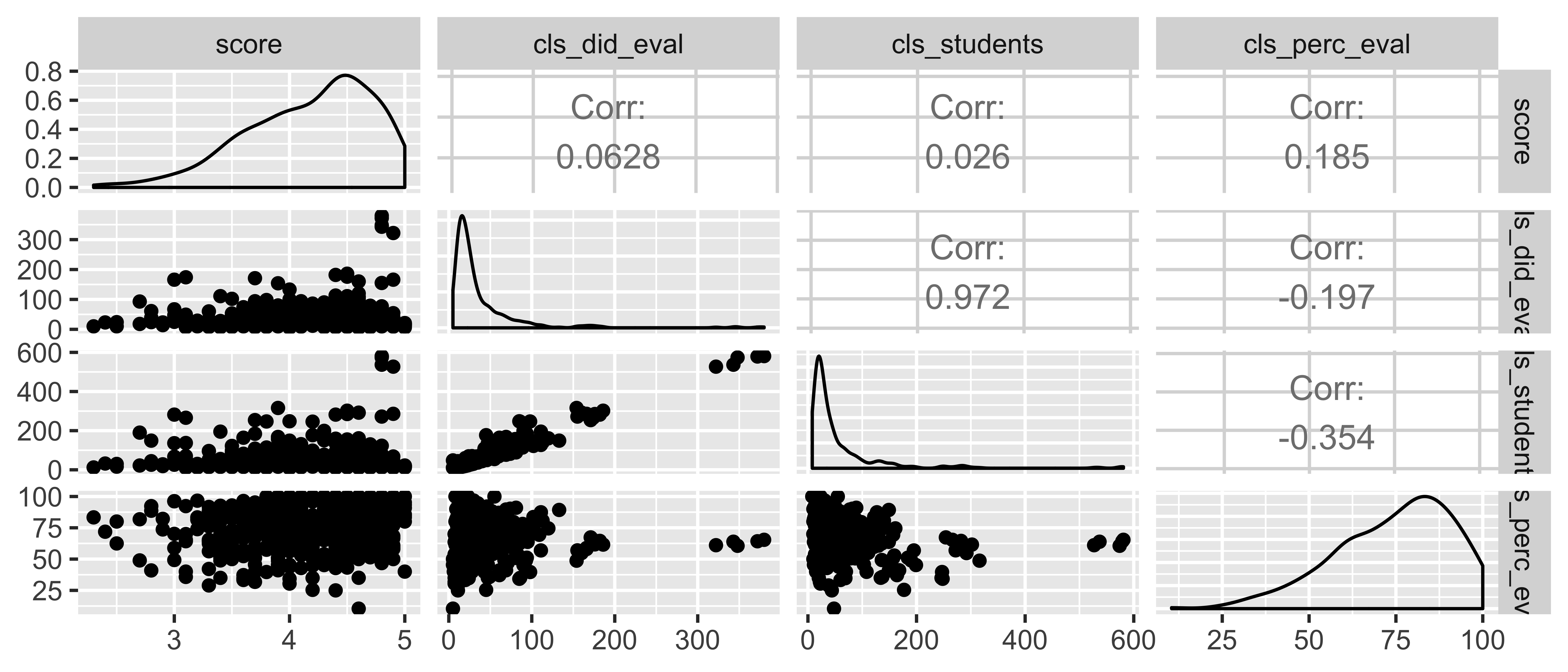
Full model
full_model <- lm(score ~ cls_did_eval + cls_students + cls_perc_eval, data = evals)glance(full_model)$adj.r.squared## [1] 0.03839408Step 1:
# Remove cls_did_evals1_stu_perc <- lm(score ~ cls_students + cls_perc_eval, data = evals)glance(s1_stu_perc)$adj.r.squared## [1] 0.03970295Step 1:
# Remove cls_did_evals1_stu_perc <- lm(score ~ cls_students + cls_perc_eval, data = evals)glance(s1_stu_perc)$adj.r.squared## [1] 0.03970295# Remove cls_studentss1_did_perc <- lm(score ~ cls_did_eval + cls_perc_eval, data = evals)glance(s1_did_perc)$adj.r.squared## [1] 0.04038255Step 1:
# Remove cls_did_evals1_stu_perc <- lm(score ~ cls_students + cls_perc_eval, data = evals)glance(s1_stu_perc)$adj.r.squared## [1] 0.03970295# Remove cls_studentss1_did_perc <- lm(score ~ cls_did_eval + cls_perc_eval, data = evals)glance(s1_did_perc)$adj.r.squared## [1] 0.04038255# Remove cls_perc_evals1_did_stu <- lm(score ~ cls_did_eval + cls_students, data = evals)glance(s1_did_stu)$adj.r.squared## [1] 0.02206412Given the following adjusted R-squared values, which model should be selected in step 1 of backwards selection?
# full modelglance(full_model)$adj.r.squared## [1] 0.03839408# remove cls_did_evalglance(s1_stu_perc)$adj.r.squared## [1] 0.03970295# remove cls_studentsglance(s1_did_perc)$adj.r.squared## [1] 0.04038255# remove cls_perc_evalglance(s1_did_stu)$adj.r.squared## [1] 0.02206412--
Removing cls_students (number of students in the class) resulted in the
highest increase in adjusted R-squared, so the model with only cls_did_eval
and cls_perc_eval (number and percentage of students who completed evaluations,
respectively) should be selected.
Step 2:
# Remove cls_did_evals2_perc <- lm(score ~ cls_perc_eval, data = evals)glance(s2_perc)$adj.r.squared## [1] 0.0321918Step 2:
# Remove cls_did_evals2_perc <- lm(score ~ cls_perc_eval, data = evals)glance(s2_perc)$adj.r.squared## [1] 0.0321918# Remove cls_perc_evals2_did <- lm(score ~ cls_did_eval, data = evals)glance(s2_did)$adj.r.squared## [1] 0.001785817Step 2:
# Remove cls_did_evals2_perc <- lm(score ~ cls_perc_eval, data = evals)glance(s2_perc)$adj.r.squared## [1] 0.0321918# Remove cls_perc_evals2_did <- lm(score ~ cls_did_eval, data = evals)glance(s2_did)$adj.r.squared## [1] 0.001785817No further variables should be dropped since dropping any results in a decrease in adjusted R-squared. The model selected in the previous step should be the final model.
Given the following adjusted R-squared values, which model should be selected in step 2 of backwards selection?
glance(s1_did_perc)$adj.r.squared # result of step 1## [1] 0.04038255glance(s2_perc)$adj.r.squared # remove cls_did_eval## [1] 0.0321918glance(s2_did)$adj.r.squared # remove cls_perc_eval## [1] 0.001785817A more realistic view: score ~ lots of variables
What percent of the variability in evaluation scores is explained by the model?
full_model <- lm(score ~ rank + ethnicity + gender + language + age + cls_perc_eval + cls_did_eval + cls_students + cls_level + cls_profs + cls_credits + bty_avg, data = evals)glance(full_model)$r.squared## [1] 0.1644867glance(full_model)$adj.r.squared## [1] 0.1402959Step 1
Given that the adjusted R-squared of the full model was 0.1403, which of the following models should be selected in the first step of backwards selection?
## remove adj_r_sq## 1 Remove cls_profs 0.1421885## 2 Remove cls_level 0.1421425## 3 Remove cls_students 0.1417647## 4 Remove cls_did_eval 0.1412196## 5 Remove rank 0.1411639## 6 Remove language 0.1394560## 7 Remove age 0.1335567## 8 Remove cls_perc_eval 0.1327892## 9 Remove ethnicity 0.1315133## 10 Remove gender 0.1187097## 11 Remove bty_avg 0.1167521## 12 Remove cls_credits 0.1064995Step 1
Given that the adjusted R-squared of the full model was 0.1403, which of the following models should be selected in the first step of backwards selection?
## remove adj_r_sq## 1 Remove cls_profs 0.1421885## 2 Remove cls_level 0.1421425## 3 Remove cls_students 0.1417647## 4 Remove cls_did_eval 0.1412196## 5 Remove rank 0.1411639## 6 Remove language 0.1394560## 7 Remove age 0.1335567## 8 Remove cls_perc_eval 0.1327892## 9 Remove ethnicity 0.1315133## 10 Remove gender 0.1187097## 11 Remove bty_avg 0.1167521## 12 Remove cls_credits 0.1064995Remove cls_profs
Step 2
Given that the adjusted R-squared of the model selected in Step 1 was 0.1422, which of the following models should be selected in the first step of backwards selection?
## remove adj_r_sq## 1 Remove cls_level 0.1440303## 2 Remove cls_students 0.1436317## 3 Remove cls_did_eval 0.1430708## 4 Remove rank 0.1430366## 5 Remove language 0.1413504## 6 Remove age 0.1354409## 7 Remove cls_perc_eval 0.1346513## 8 Remove ethnicity 0.1329045## 9 Remove gender 0.1206375## 10 Remove bty_avg 0.1187028## 11 Remove cls_credits 0.1078684Step 2
Given that the adjusted R-squared of the model selected in Step 1 was 0.1422, which of the following models should be selected in the first step of backwards selection?
## remove adj_r_sq## 1 Remove cls_level 0.1440303## 2 Remove cls_students 0.1436317## 3 Remove cls_did_eval 0.1430708## 4 Remove rank 0.1430366## 5 Remove language 0.1413504## 6 Remove age 0.1354409## 7 Remove cls_perc_eval 0.1346513## 8 Remove ethnicity 0.1329045## 9 Remove gender 0.1206375## 10 Remove bty_avg 0.1187028## 11 Remove cls_credits 0.1078684Remove cls_level
Step 3
Given that the adjusted R-squared of the model selected in Step 2 was 0.144, which of the following models should be selected in the first step of backwards selection?
## remove adj_r_sq## 1 Remove cls_students 0.1453516## 2 Remove rank 0.1449154## 3 Remove cls_did_eval 0.1447586## 4 Remove language 0.1432499## 5 Remove age 0.1373534## 6 Remove cls_perc_eval 0.1365490## 7 Remove ethnicity 0.1344177## 8 Remove gender 0.1225830## 9 Remove bty_avg 0.1206257## 10 Remove cls_credits 0.1076569Step 3
Given that the adjusted R-squared of the model selected in Step 2 was 0.144, which of the following models should be selected in the first step of backwards selection?
## remove adj_r_sq## 1 Remove cls_students 0.1453516## 2 Remove rank 0.1449154## 3 Remove cls_did_eval 0.1447586## 4 Remove language 0.1432499## 5 Remove age 0.1373534## 6 Remove cls_perc_eval 0.1365490## 7 Remove ethnicity 0.1344177## 8 Remove gender 0.1225830## 9 Remove bty_avg 0.1206257## 10 Remove cls_credits 0.1076569Remove cls_students
Step 4
Given that the adjusted R-squared of the model selected in Step 3 was 0.1454, which of the following models should be selected in the first step of backwards selection?
## remove adj_r_sq## 1 Remove rank 0.1460210## 2 Remove language 0.1447503## 3 Remove cls_did_eval 0.1438601## 4 Remove age 0.1386372## 5 Remove ethnicity 0.1351420## 6 Remove gender 0.1244633## 7 Remove bty_avg 0.1220691## 8 Remove cls_perc_eval 0.1216729## 9 Remove cls_credits 0.1091898Step 4
Given that the adjusted R-squared of the model selected in Step 3 was 0.1454, which of the following models should be selected in the first step of backwards selection?
## remove adj_r_sq## 1 Remove rank 0.1460210## 2 Remove language 0.1447503## 3 Remove cls_did_eval 0.1438601## 4 Remove age 0.1386372## 5 Remove ethnicity 0.1351420## 6 Remove gender 0.1244633## 7 Remove bty_avg 0.1220691## 8 Remove cls_perc_eval 0.1216729## 9 Remove cls_credits 0.1091898Remove rank
Step 5
Given that the adjusted R-squared of the model selected in Step 3 was 0.146, which of the following models should be selected in the first step of backwards selection?
## remove adj_r_sq## 1 Remove cls_did_eval 0.1445941## 2 Remove language 0.1438720## 3 Remove age 0.1413323## 4 Remove ethnicity 0.1340933## 5 Remove gender 0.1245360## 6 Remove bty_avg 0.1218780## 7 Remove cls_perc_eval 0.1216266## 8 Remove cls_credits 0.1010899Step 5
Given that the adjusted R-squared of the model selected in Step 3 was 0.146, which of the following models should be selected in the first step of backwards selection?
## remove adj_r_sq## 1 Remove cls_did_eval 0.1445941## 2 Remove language 0.1438720## 3 Remove age 0.1413323## 4 Remove ethnicity 0.1340933## 5 Remove gender 0.1245360## 6 Remove bty_avg 0.1218780## 7 Remove cls_perc_eval 0.1216266## 8 Remove cls_credits 0.1010899None, stick with model from Step 4.
Final model
## # A tibble: 9 x 2## term estimate## <chr> <dbl>## 1 (Intercept) 3.41 ## 2 ethnicitynot minority 0.202 ## 3 gendermale 0.177 ## 4 languagenon-english -0.151 ## 5 age -0.00487 ## 6 cls_perc_eval 0.00549 ## 7 cls_did_eval 0.000722## 8 cls_creditsone credit 0.524 ## 9 bty_avg 0.0615Model selection and interaction effects
Model selection for models including interaction effects must follow the following two principles:
- If an interaction is included in the model, the main effects of both of those variables must also be in the model.
- If a main effect is not in the model, then its interaction should not be in the model.
Other model selection criteria
- Adjusted R-squared is one model selection criterion
- There are others out there (many many others!), we'll discuss one more in this course, and you'll learn about others in future stats courses
Akaike Information Criterion
AIC=−2log(L)+2k
- L: likelihood of the model
- Likelihood of seeing these data given the estimated model parameters
- Won't go into calculating it in this course (but you will in future courses)
- Used for model selection, lower the better
- Value is not informative on its own
- Applies a penalty for number of parameters in the model, k
- Different penalty than adjusted R2 but similar idea
glance(full_model)$AIC## [1] 695.7457Model selection -- a little faster
step() function selects a model by AIC:
selected_model <- step(full_model, direction = "backward")tidy(selected_model) %>% select(term, estimate)## # A tibble: 8 x 2## term estimate## <chr> <dbl>## 1 (Intercept) 3.45 ## 2 ethnicitynot minority 0.205 ## 3 gendermale 0.185 ## 4 languagenon-english -0.161 ## 5 age -0.00501## 6 cls_perc_eval 0.00509## 7 cls_creditsone credit 0.515 ## 8 bty_avg 0.0650AIC comparison
glance(full_model)$AIC## [1] 695.7457glance(selected_model)$AIC## [1] 687.5712Parsimony
Take a look at the variables in the full and the selected model. Can you guess why some of them may have been dropped? Remember: We like parsimonous models.
| variable | selected |
|---|---|
| rank | |
| ethnicity | x |
| gender | x |
| language | x |
| age | x |
| cls_perc_eval | x |
| cls_did_eval | |
| cls_students | |
| cls_level | |
| cls_profs | |
| cls_credits | x |
| bty_avg | x |
Interpretation
Interpret the slope of bty_avg and gender in the selected model.
## # A tibble: 8 x 2## term estimate## <chr> <dbl>## 1 (Intercept) 3.45 ## 2 ethnicitynot minority 0.205 ## 3 gendermale 0.185 ## 4 languagenon-english -0.161 ## 5 age -0.00501## 6 cls_perc_eval 0.00509## 7 cls_creditsone credit 0.515 ## 8 bty_avg 0.0650Interpretation
Interpret the slope of bty_avg and gender in the selected model.
## # A tibble: 8 x 2## term estimate## <chr> <dbl>## 1 (Intercept) 3.45 ## 2 ethnicitynot minority 0.205 ## 3 gendermale 0.185 ## 4 languagenon-english -0.161 ## 5 age -0.00501## 6 cls_perc_eval 0.00509## 7 cls_creditsone credit 0.515 ## 8 bty_avg 0.0650- All else held constant, for each additional point in beauty score, the evaluation score of the professor is predicted to be higher, on average, by 0.06 points.
Interpretation
Interpret the slope of bty_avg and gender in the selected model.
## # A tibble: 8 x 2## term estimate## <chr> <dbl>## 1 (Intercept) 3.45 ## 2 ethnicitynot minority 0.205 ## 3 gendermale 0.185 ## 4 languagenon-english -0.161 ## 5 age -0.00501## 6 cls_perc_eval 0.00509## 7 cls_creditsone credit 0.515 ## 8 bty_avg 0.0650- All else held constant, for each additional point in beauty score, the evaluation score of the professor is predicted to be higher, on average, by 0.06 points.
- All else held constant, male professors are predicted to score higher on their evaluation score than female professors by 0.185 points.